Qu’est-ce que la cryptographie à courbe elliptique ?

La cryptographie à courbe elliptique (ECC) est une forme de cryptographie à clé publique basée sur les mathématiques des courbes elliptiques. Elle fournit un moyen sécurisé d’effectuer des opérations cryptographiques telles que l’échange de clés, les signatures numériques et le chiffrement. L’ECC est une alternative au chiffrement Rivest-Shamir-Adleman (RSA), qui a été mis sur le marché pour la première fois en 1977.

Poursuivez votre lecture pour en savoir plus sur la cryptographie à courbe elliptique et pourquoi elle est considérée comme la forme de chiffrement la plus sécurisée.

Quelle est la différence entre ECC et RSA ?

Avant d’examiner les différences entre ECC et RSA, il est important de comprendre le fonctionnement des algorithmes cryptographiques à clé publique. Dans leur forme la plus élémentaire, les algorithmes cryptographiques robustes sont des « fonctions de trappe ». Il est très facile de tomber dans une trappe, mais très difficile d’en ressortir, car les trappes ne s’ouvrent que dans une seule direction. Ainsi, pour qu’un algorithme cryptographique soit efficace et sûr, il doit permettre de chiffrer facilement un message, mais rendre presque impossible son déchiffrement sans la clé de déchiffrement.

L’ECC et le RSA sont des algorithmes de chiffrement à clé publique qui s’appuient sur des fonctions mathématiques très avancées. Le chiffrement à clé publique comporte deux composants : une clé publique et une clé privée. La clé publique permet de chiffrer un message en appliquant un algorithme mathématique qui le transforme en un très grand chiffre d’apparence aléatoire. Le message ne peut être déchiffré que grâce à la clé privée, qui applique au nombre aléatoire un algorithme différent qui « annule » l’original.

Les mathématiques à l’origine de l’ECC et du RSA sont si complexes qu’elles ne peuvent être résolues que par des ordinateurs. Les mathématiques qui sous-tendent l’algorithme RSA dépassent le cadre de ce blog, mais l’essentiel à retenir est que la sécurité du RSA dépend de l’immense difficulté à factoriser de très grands nombres en leurs nombres premiers composés.

Petit rappe : la factorisation d’un nombre comme 20 ressemble à ceci :

20 = 4 * 5 = 2 * 2 * 5 = 2² * 5

Cela a l’air simple, n’est ce pas ? Imaginez maintenant que vous devez le faire avec un nombre de plus de 100 chiffres. C’est pourquoi, même avec une clé publique, il est extrêmement difficile de calculer la clé privée sans connaître les facteurs premiers.

Les problèmes liés à la cryptographie RSA

Bien que l’algorithme RSA soit assez robuste, il pose quelques problèmes.

La factorisation de très grands nombres est extrêmement difficile, mais elle l’est moins qu’auparavant. La factorisation est un élément essentiel du calcul et d’autres mathématiques avancées. Les mathématiciens ont donc passé des siècles à chercher des moyens de la rendre plus facile. Il existe des algorithmes efficaces pour factoriser les grands nombres, comme le General Number Field Sieve, qui est actuellement la méthode la plus connue pour factoriser les grands nombres de plus de 110 chiffres.

Dans le même temps, la puissance de calcul s’accroît à une vitesse fulgurante. En 1965, Gordon Moore, cofondateur d’Intel, a prédit que le nombre de transistors sur une puce électronique doublerait tous les ans ou tous les deux ans. Cette hypothèse est connue sous le nom de loi de Moore et, depuis les années 1970, elle est respectée, voire dépassée. La puissance de calcul double tous les deux ans environ, et son prix diminue.

Comme les ressources informatiques nécessaires pour factoriser des nombres extrêmement importants deviennent plus facilement accessibles et abordables pour une grande partie du public (y compris les cybercriminels), la taille des clés RSA doit augmenter pour suivre le mouvement. C’est pourquoi les vitesses de chiffrement et de déchiffrement RSA sont plutôt lentes, ce qui rend son utilisation impossible pour le chiffrement de messages volumineux, en particulier sur les appareils mobiles. En revanche, la méthode RSA est couramment utilisée pour l’échange de clés et les signatures numériques, où les données réelles sont chiffrées à l’aide d’algorithmes de chiffrement symétriques avec des clés de session à durée de vie plus courte.

À l’inverse, la cryptographie à courbe elliptique offre sans doute une meilleure sécurité avec des longueurs de clé plus courtes, ce qui la rend plus efficace en termes de calcul et de bande passante. Nous allons examiner le fonctionnement de l’ECC dans la section suivante.

Comment fonctionne la cryptographie à courbe elliptique ?

L’ECC se fonde sur un autre domaine des mathématiques avancées : les courbes elliptiques. Une courbe elliptique est définie par une équation de la forme y² = x³ + ax + b, où a et b sont des constantes et où la courbe est définie sur un corps fini. La représentation graphique est la suivante :

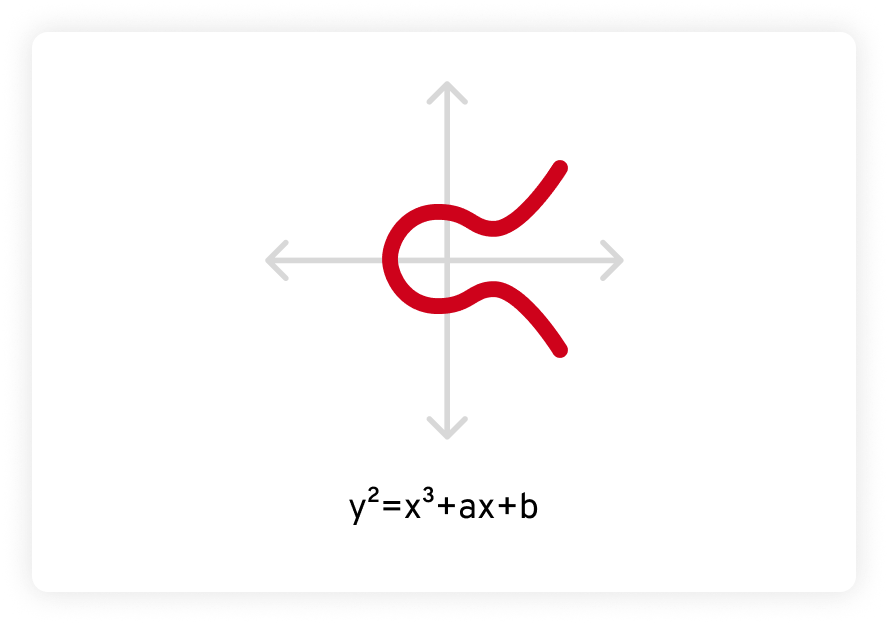
Les courbes elliptiques ont des propriétés spéciales qui les rendent intéressantes et utiles pour les mathématiciens et les cryptographes. Tout d’abord, les courbes elliptiques sont à symétrie horizontale. Lorsque l’image est réfléchie sur l’axe des x (la ligne horizontale), les deux côtés sont identiques, comme une image miroir.

En outre, toute ligne droite non verticale tracée à travers une courbe elliptique l’intersectera toujours en trois points au maximum. Dans l’exemple ci-dessous, ces points sont marqués P, Q et R.

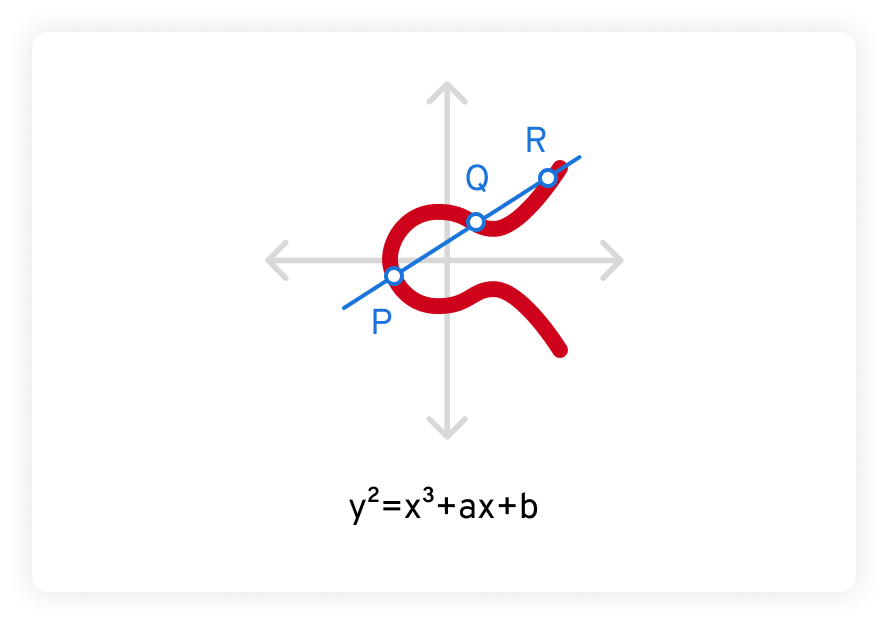
La sécurité de la cryptographie à courbe elliptique repose sur la difficulté de résoudre ce que l’on appelle le problème du logarithme discret de la courbe elliptique. Étant donné un point P sur la courbe et un scalaire k, il est incroyablement difficile de déterminer le point Q tel que Q = k*P. Beaucoup plus difficile que de factoriser même un très grand nombre.

Cette propriété signifie que l’ECC peut fournir une sécurité comparable, voire meilleure, que l’algorithme RSA avec des clés de taille bien inférieure.

Les avantages de la cryptographie à courbe elliptique

Le fait que l’ECC offre un très haut niveau de sécurité avec des longueurs de clés courtes lui confère des avantages par rapport au chiffrement RSA et à d’autres algorithmes de cryptographie à clé publique.

Voici deux avantages liés à l’utilisation de la cryptographie à courbe elliptique.

• L’ECC nécessite moins de ressources informatiques et moins de bande passante pour la génération de clé, le chiffrement et le déchiffrement.
• En raison de la taille réduite de la clé ECC, les opérations ECC (telles que la génération de clés, le chiffrement et le déchiffrement) peuvent être effectuées plus rapidement qu’avec la cryptographie RSA, ce qui signifie moins de temps de latence pour l’utilisateur final.

Ces avantages rendent l’ECC particulièrement utile dans les environnements à ressources limitées, tels que les appareils mobiles et ceux de l’Internet des objets (IoT).

À quel point la cryptographie à courbe elliptique est-elle sécurisée ?

L’algorithme de chiffrement RSA est certes extrêmement sécurisé, mais l’algorithme ECC est sans doute encore meilleur.

Les ordinateurs quantiques ont théoriquement la possibilité de décoder le système RSA en résolvant efficacement le problème de factorisation sur lequel repose le système RSA. La question de savoir si cela se produira dans un avenir proche fait l’objet d’un débat intense. Toutefois, nous pouvons dire avec certitude qu’en raison de sa complexité, l’algorithme ECC est plus résistant aux attaques par informatique quantique que l’algorithme RSA.

À quel point la cryptographie ECC est-elle résistante ? Le mathématicien néerlandais Arjen Lenstra a coécrit une étude qui comparait le fait de décoder des algorithmes cryptographiques à faire bouillir de l’eau. L’idée est de calculer la quantité d’énergie nécessaire pour décoder un algorithme cryptographique donné, puis de calculer la quantité d’eau que cette énergie pourrait faire bouillir. Pour reprendre cette métaphore, il faut moins d’énergie pour décoder une clé RSA de 228 bits que pour faire bouillir une cuillère à café d’eau, tandis que l’énergie dépensée pour décoder une clé ECC de 228 bits pourrait faire bouillir toute l’eau de la Terre. Le même niveau de sécurité avec le RSA nécessiterait une taille de clé de 2 380 bits.

Domaines d’utilisation de la cryptographie à courbe elliptique

Comme nous l’avons déjà mentionné, la taille réduite des clés ECC en fait une solution idéale pour les appareils dotés de faibles ressources en termes de CPU et de mémoire, tels que les appareils mobiles et IoT. Cela permet aux développeurs de sites Web et d’applications mobiles de créer des sites Web et des applications très performants et à faible latence, tout en offrant à leurs utilisateurs une sécurité des données élevée. L’ECC est fréquemment utilisée pour sécuriser les protocoles de communication mobile sans fil tels que le Bluetooth, le Wi-Fi et le Near Field Communication (NFC).

Voici quelques cas d’usage courants de l’ECC :

• Les protocoles de communication sécurisés : l’ECC est utilisée dans divers protocoles de communication sécurisés pour assurer le chiffrement, les signatures numériques et l’échange de clés. Il s’agit par exemple de la sécurité de la couche de transport (TLS) utilisée pour sécuriser la navigation sur le Web, de Secure Shell (SSH) pour sécuriser la connexion à distance et des réseaux privés virtuels (VPN) pour sécuriser la communication réseau.
• Les crypto-monnaies et la technologie blockchain : de nombreuses crypto-monnaies, dont le Bitcoin, l’Ethereum et le Litecoin, utilisent la cryptographie à courbe elliptique pour générer des paires de clés publiques et privées, ainsi que pour signer les transactions. L’ECC fournit la sécurité cryptographique nécessaire pour sécuriser les actifs numériques et garantir l’intégrité des réseaux de blockchain.
• Les cartes à puce et les systèmes intégrés : l’ECC est couramment utilisée pour sécuriser les systèmes de paiement, les systèmes de contrôle d’accès, les passeports électroniques et d’autres applications qui nécessitent des solutions cryptographiques sûres et compactes.
• Les signatures numériques et les certificats : l’ECC peut être utilisée pour générer des signatures numériques, qui servent à vérifier l’authenticité et l’intégrité des documents et des messages numériques. Les signatures numériques basées sur l’ECC sont également utilisées dans les systèmes d’infrastructure à clé publique (PKI) pour émettre et valider les certificats numériques.

Bien que l’ECC soit plutôt nouvelle par rapport au RSA, elle bénéficie d’une large normalisation et d’un soutien de la part des organisations du secteur privé et des organismes sectoriels. Le National Institute of Standards and Technology (NIST) des États-Unis a par exemple normalisé l’ECC dans sa suite d’algorithmes cryptographiques. En outre, l’ECC est pris en charge par les bibliothèques cryptographiques, les langages de programmation et les systèmes d’exploitation les plus répandus. Ce phénomène favorise son adoption dans divers secteurs tels que la finance, les soins de santé et les services gouvernementaux.

Compte tenu de ces facteurs, nous pouvons affirmer sans hésiter que la cryptographie à courbe elliptique est populaire et largement utilisée dans un grand nombre d’applications et de secteurs d’activité. Son efficacité, sa sécurité et sa prise en charge générale en ont fait un choix de confiance pour les communications sécurisées et les opérations cryptographiques.