楕円曲線暗号(ECC)とは何か？

楕円曲線暗号（ECC）は、英語圏では「Elliptic Curve Cryptography」と表記し、楕円曲線と呼ばれる数学上の概念に基づいた公開鍵暗号の一形態です。鍵交換、デジタル署名、暗号化などの暗号操作を、安全な方法で行うことができます。ECC は、1977 年に初めてリリースされた Rivest-Shamir-Adleman（RSA）暗号の代替物です。

最近ではビットコインをはじめとする暗号通貨に楕円曲線暗号が暗号化方式として採用されており、知った人も多いのではないでしょうか。

楕円曲線暗号の分かりやすい特徴としては、RSAより短い暗号鍵でも高い安全性を確保できるとされており、計算能力が低いコンピューターでも実装できることです。

楕円曲線暗号とそれが最も安全な暗号化形式だと考えられている理由を、さらに詳しく説明します。

楕円曲線暗号の仕組みとは？

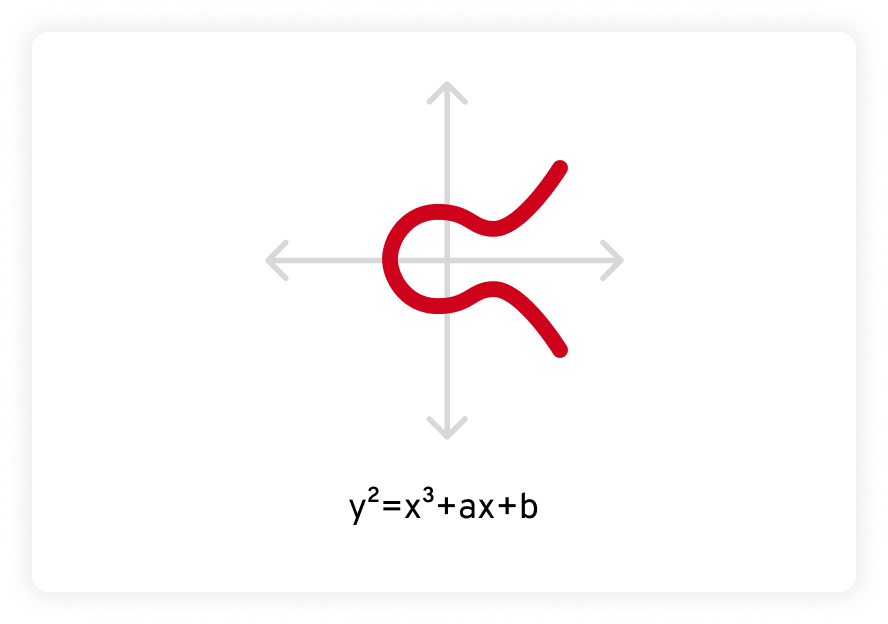
ECC は、楕円曲線と呼ばれる別の先進数学の分野に基づいています。楕円曲線は y² = x³ + ax + b という形式の方程式で定義され、a と b は定数であり、曲線は有限体上で定義されます。グラフ化すると、次のようになります。

楕円曲線には、数学者と暗号学者の両者にとって興味深く有用な複数の特別な性質があります。第一に、楕円曲線は水平対称です。X 軸（水平線）で折り返すと、両側が鏡のように同じになります。

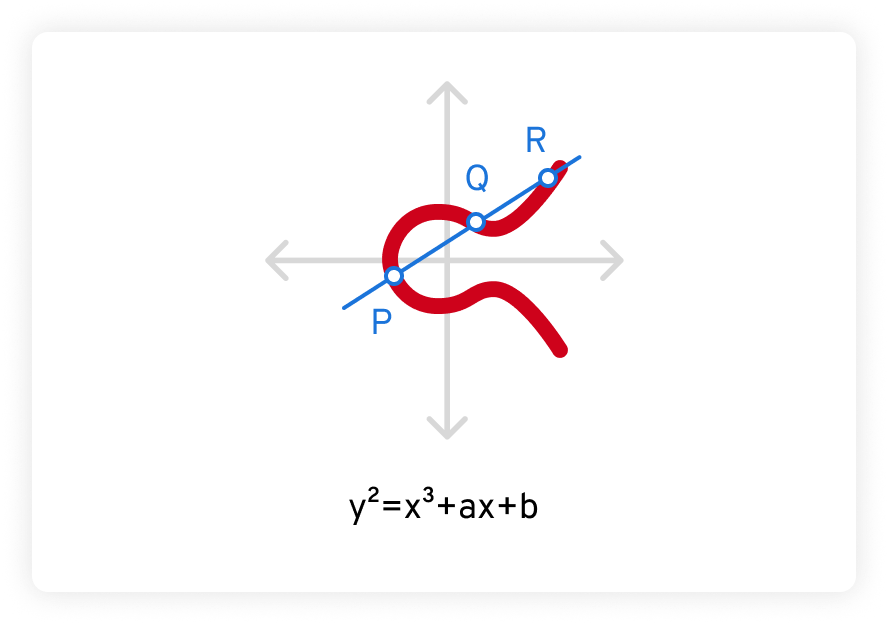
さらに、楕円曲線を介して描かれた非垂直の直線は、最大 3 つの場所で曲線と交差します。以下の例では、これらの点は P、Q、R とラベル付けされています。

楕円曲線暗号のセキュリティは、楕円曲線離散対数問題として知られている問題を解決することの困難さに基づいています。曲線上の点 P とスカラー k が与えられると、Q = k*P を満たす点 Q を決定するのは非常に困難です。非常に大きな数を因数分解するよりもはるかに困難です。

この性質は、ECC がはるかに小さい鍵サイズで、RSAと同等、あるいはより良いセキュリティを提供できることを意味します。

RSA暗号に関する問題

RSAアルゴリズムは非常に堅牢ですが、問題が無いわけではありません。

非常に大きな数を因数分解するのは非常に困難ですが、以前よりは難しくなくなっています。因数分解は微積分やその他の先進数学の中核要素であり、数学者は何世紀にもわたってそれを容易にする方法を模索してきました。一般数フィールドシーブのように、大きな数を因数分解するのに効率的なアルゴリズムが存在します。これは現在、110 桁を超える大きな数を因数分解する最も有名な方法です。

一方で、計算能力は驚異的な速度で拡大しています。1965年、Intel の共同設立者であるゴードン・ムーアは、マイクロチップ上のトランジスタの数が毎年もしくは 2 年で倍増する、と予測しました。この仮説はムーアの法則として知られており、1970 年代から的中しているか、さらに超過しています。計算能力は約 2 年ごとに倍増し、計算能力の価格は低下しています。

非常に大きな数を因数分解するのに必要な計算資源が容易に入手可能になり、（サイバー犯罪者を含む）一般向けに手頃な価格になっているため、RSAキーのサイズは拡大する必要があります。このため、RSA は暗号化と復号化の速度がかなり遅く、特にモバイルデバイス上では大きなメッセージの暗号化を実現できません。代わりに、RSAは鍵交換やデジタル署名に広く使用されており、実際のデータはより短時間のセッションキーを持つ対称暗号化アルゴリズムを使用して暗号化されます。

それとは逆に、楕円曲線暗号は鍵が短いことで間違いなくより良いセキュリティを提供しており、計算と帯域幅要件の点でより効率的です。

ECCとRSAの違いは？

• 楕円曲線暗号（Elliptic Curve Cryptography）
• RSA暗号（Rivest-Shamir-Adleman）三人の頭文字を取った表記

ECCとRSAの違いを議論する前に、公開鍵暗号アルゴリズムの仕組みを理解しておくことが重要です。最も基本的で堅牢な暗号アルゴリズムは、「トラップドア関数」です。トラップドアをある方向に通り抜けることはとても簡単ですが、ドアはその方向にしか開かないため、逆方法に通り抜けることは非常に困難です。このように、暗号アルゴリズムが効果的かつ安全であるためにはメッセージの暗号化が容易でなければなりませんが、非暗号化鍵なしで復号化することはほぼ不可能です。

ECCとRSAはどちらも、非常に高度な数学関数を使用する公開鍵暗号アルゴリズムです。公開鍵の暗号化には、公開鍵と秘密鍵の 2 つのコンポーネントがあります。公開鍵はメッセージを暗号化し、数学的なアルゴリズムを適用して、非常に大きくランダムに出現する番号に変換します。メッセージは秘密鍵でのみ復号化できます。この秘密鍵はランダムに現れる数字を受け取り、基本的に「元に戻す」異なるアルゴリズムを適用します。

ECCとRSAの背後にある数学は非常に複雑で、コンピュータを使用してのみ解決が可能です。RSA アルゴリズムの背後にある数学はこのブログの範疇外ですが、最も重要なのはRSAのセキュリティが非常に大きな数を合成素数に分解する、という大きな困難さに依存しているということです。

おさらいが必要な人のために、例えば20を因数分解すると、次のようになります。

20 = 4 x 5 = 2 x 2 x 5 = 2² x 5

簡単そうですよね？では、100 桁以上の数字での計算を想像してください。このような理由で、公開鍵があっても素因数が分からないまま秘密鍵を計算すると、非常に計算量が多くなるのです。

楕円曲線暗号のメリット

ECCが短い鍵で非常に高いレベルのセキュリティを提供しているという事実により、楕円曲線暗号はRSAや他の公開鍵暗号アルゴリズムよりも優位性を有しています。

楕円曲線暗号を使用するメリットを2つご紹介します。

●   ECCでは、鍵生成、暗号化、復号化の計算リソースが少なくて済み、帯域幅も少なくなります。

●   ECCの鍵サイズは小さいため、鍵生成、暗号化、復号化などの操作を RSA と比べて高速で行うことができ、これはエンドユーザーの待ち時間が少ないことを意味します。

このようなメリットから、ECCはモバイルやモノのインターネット（IoT）デバイスのようなリソースに制約のある環境では特に有用です。

楕円曲線暗号の安全性は？

RSA暗号化アルゴリズムは非常に安全ではあるものの、ECCは間違いなくそのさらに上を行く安全性を持っています。

量子コンピュータは理論的には、RSAが依存するファクタリング問題を効率的に解決することで、RSA を破る可能性があります。このことが間もなく起こるかどうかは、大きな議論の的となっています。しかし、ECC はその複雑さにより、RSAに比べて量子コンピューティング攻撃に対してより耐性があると言っても過言ではありません。

どれほど耐性があるか？オランダの数学者Arjen Lenstraが共同執筆した研究論文の中で、暗号アルゴリズムの解読と水の沸騰が比較されました。その考えとは、特定の暗号アルゴリズムを解読するのに必要なエネルギー量を計算し、それから沸騰する水の量を計算するという内容です。このメタファーを使用すると、ティースプーン 1杯の水を沸騰させるよりも、228ビットの RSA鍵を解読するのにかかるエネルギーが少ない一方で、228ビットの ECC鍵を解読するエネルギーは、地球上のすべての水を沸騰させる可能性があります。RSAと同じレベルのセキュリティでは、2,380ビットの鍵サイズが必要になります。

楕円曲線暗号が使用される場所

前述したように、ECCの鍵サイズは小さいため、モバイルや IoT デバイスなど、CPUやメモリリソースの少ないデバイスに最適です。これにより、ウェブやモバイルアプリの開発者は、高性能で低レイテンシーなウェブサイトやアプリケーションを構築でき、同時にユーザーに堅牢なデータセキュリティを提供できます。ECCは、Bluetooth、Wi-Fi、近距離無線通信（NFC）のような無線通信プロトコルの保護に頻繁に使用されます。

ECCの一般的なユースケースを、いくつかご紹介します。

●   安全な通信プロトコル：ECCは、暗号化、デジタル署名、鍵交換を提供するために、さまざまな安全な通信プロトコルで使用されています。例えば、安全なウェブブラウジングで使用されるトランスポート層セキュリティ（TLS）、安全なリモートログイン用のセキュアシェル（SSH）、安全なネットワーク通信用の仮想プライベートネットワーク（VPN）などがあります。

●   暗号通貨とブロックチェーン技術：Bitcoin、Ethereum、Litecoin を含む多くの暗号通貨は、楕円曲線暗号を公開鍵と秘密鍵ペアの生成、ならびにトランザクションの署名に使用します。ECC は、デジタル資産を保護し、ブロックチェーンネットワークの完全性を確保するために必要な暗号セキュリティを提供します。

●  スマートカードと組込みシステム：ECCは、決済システム、アクセス制御システム、電子パスポート、そして安全でコンパクトな暗号ソリューションを必要とするその他のアプリ保護に広く使用されています。

●  デジタル署名と証明書：ECCはデジタル署名の生成に使用でき、デジタルドキュメントやメッセージの真正性と完全性を検証するために使用されます。ECCベースのデジタル署名は、デジタル証明書を発行し検証するために、公開鍵インフラストラクチャ（PKI）システムでも採用されています。

ECCはRSAに比べてかなり新しい暗号方式ですが、民間組織や業界団体から幅広い標準化とサポートを受けています。例えば、米国国立標準技術研究所（NIST）は、暗号アルゴリズムスイートで ECCを標準化しています。さらに ECCは、人気のある暗号ライブラリ、プログラミング言語、オペレーティングシステムでサポートされています。この受け入れ状況により、金融、医療、政府サービスなど様々な分野での採用がさらに促進されます。

まとめ：楕円曲線暗号は幅広く応用されている

楕円曲線暗号は人気が高く、さまざまなアプリケーションや業界で広く使用されていると言っても過言ではありません。その効率、セキュリティ、幅広いサポートにより、安全な通信と暗号運用のための信頼できる選択肢となっています。

またサイバーセキュリティを理解していく上で、重要な要素なので皆様に少しでも理解を深めることができると幸いです。

この機会にKeeperパスワードマネージャーの無料30日間トライアル体験または、14日間のビジネスプランのフリートライアルを試してみてはいかがでしょうか。

ビジネス版: 14日間の無料体験を試す