The main difference between an attack vector and an attack surface is that an attack vector is the specific way a cybercriminal can take advantage of
Elliptic Curve Cryptography (ECC) is a form of public-key cryptography that is based on the mathematics of elliptic curves. It provides a secure way to perform cryptographic operations such as key exchange, digital signatures and encryption. ECC is an alternative to Rivest-Shamir-Adleman (RSA) encryption, which was first released in 1977.
Continue reading to learn more about elliptic curve cryptography and why it’s considered the most secure form of encryption.
What is the Difference Between ECC and RSA?
Before discussing the differences between ECC and RSA, it’s important to understand how public-key cryptographic algorithms work. At their most basic, robust cryptographic algorithms are “trapdoor functions.” While falling through a trapdoor is very easy, getting back out is very difficult because trapdoors only swing in one direction. Thus, for a cryptographic algorithm to be effective and secure, it must be easy to encrypt a message, but nearly impossible to decrypt without the decryption key.
Both ECC and RSA are public key encryption algorithms that leverage highly advanced mathematical functions. Public key encryption has two components, a public key and a private key. The public key encrypts a message by applying a mathematical algorithm to transform it into a very large, random-appearing number. The message can only be decrypted with the private key, which takes the random-appearing number and applies a different algorithm that essentially “undoes” the original.
The mathematics behind ECC and RSA are so complex, they can only be solved using computers. The mathematics behind the RSA algorithm is beyond the scope of this blog, but the crux is that RSA’s security depends on the immense difficulty of factoring very large numbers into their composite primes.
For those who need a refresher, factoring a number like 20 looks like this:
20 = 4 * 5 = 2 * 2 * 5 = 22 * 5
Looks simple, right? Now imagine doing that with a number over 100 digits long. That’s why, even with a public key, it’s extremely computationally intensive to calculate the private key without knowing the prime factors.
Issues with RSA Cryptography
While the RSA algorithm is quite robust, it’s not without issues.
Factoring very large numbers is extremely difficult, but less difficult than it used to be. Factoring is a core component of calculus and other advanced mathematics, so mathematicians have spent centuries seeking ways to make it easier. There exist efficient algorithms to factor large numbers, such as the General Number Field Sieve, which is currently the best-known method for factoring large numbers exceeding 110 digits.
Meanwhile, computational power is expanding at an astounding rate. In 1965, Intel Co-Founder Gordon Moore predicted that the number of transistors on a microchip would double every year or two. This hypothesis is known as Moore’s Law, and since the 1970s, it has been met or exceeded. Computing power doubles about every two years – and the price of computing power is going down.
As the computing resources needed to factor extremely large numbers become more readily available and affordable to a large swath of the public (including cybercriminals), RSA key sizes must grow to keep up. Because of this, RSA has rather slow encryption and decryption speeds, which makes it infeasible for encrypting large messages, especially on mobile devices. Instead, RSA is commonly used for key exchange and digital signatures, where the actual data is encrypted using symmetric encryption algorithms with shorter-lived session keys.
Conversely, elliptic curve cryptography offers arguably better security with shorter key lengths, making it more efficient in terms of computation and bandwidth requirements. We’ll examine how ECC works in the next section.
How Does Elliptic Curve Cryptography Work?
ECC is based on another area of advanced mathematics called elliptic curves. An elliptic curve is defined by an equation in the form of y2 = x3 + ax + b, where a and b are constants and the curve is defined over a finite field. When graphed, it looks like this:
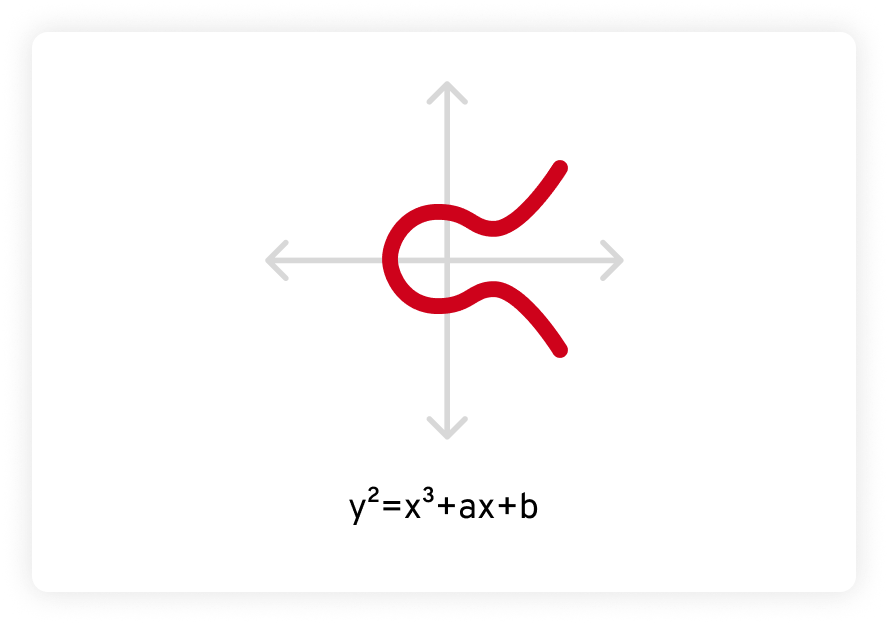
Elliptic curves have some special properties that make them interesting and useful to both mathematicians and cryptographers. First, elliptic curves are horizontally symmetrical. When reflected across the x-axis (the horizontal line), both sides are the same, like a mirror image.
Additionally, any non-vertical straight line drawn through an elliptic curve will always intersect the curve in, at most, three places. In the example below, those points are labeled as P, Q and R.
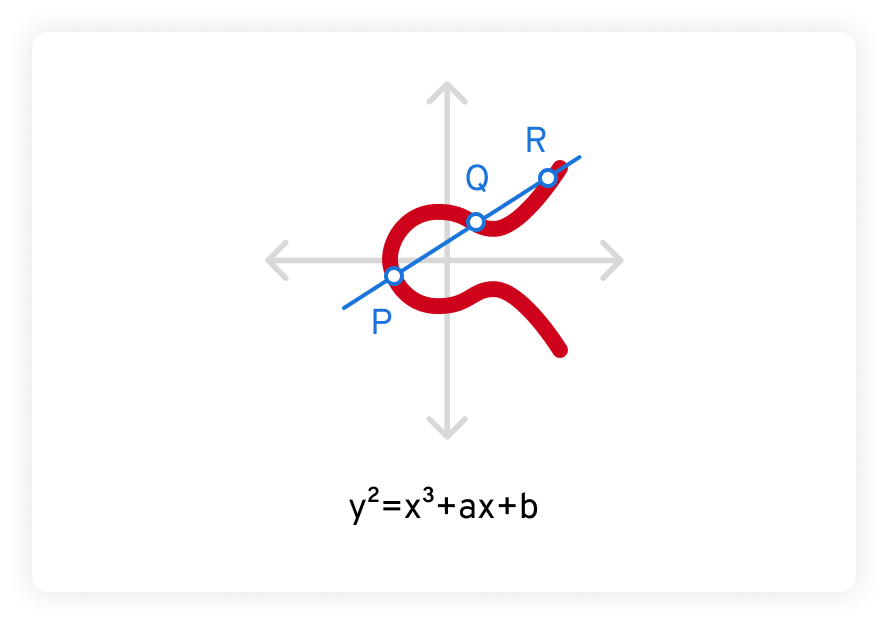
The security of elliptic curve cryptography is based on the difficulty of solving what’s known as the elliptic curve discrete logarithm problem. Given a point P on the curve and a scalar k, it is extraordinarily difficult to determine the point Q such that Q = k*P – much more difficult than it is to factor even a very large number.
This property means that ECC can provide comparable or even better security than RSA with far lower key sizes.
Benefits of Elliptic Curve Cryptography
The fact that ECC provides a very high level of security with short key lengths gives it advantages over RSA and other public-key cryptography algorithms.
Here are two benefits of using elliptic curve cryptography.
- ECC requires fewer computational resources and less bandwidth for key generation, encryption and decryption.
- Due to ECC’s smaller key size, ECC operations, such as key generation, encryption and decryption, can be performed faster compared to RSA, which means less latency for the end user.
These advantages make ECC particularly useful in resource-constrained environments, such as mobile and Internet of Things (IoT) devices.
How Secure is Elliptic Curve Cryptography?
While the RSA encryption algorithm is extremely secure, ECC is arguably even better.
Quantum computers theoretically have the potential to break RSA by efficiently solving the factoring problem on which RSA relies. Whether this will happen anytime soon is a matter of great debate. However, it is safe to say that, due to ECC’s complexity, it is more resistant to quantum computing attacks compared to RSA.
How resistant? Dutch mathematician Arjen Lenstra co-wrote a research paper that compared breaking cryptographic algorithms to boiling water. The idea is to compute how much energy it requires to break a specific cryptographic algorithm, then calculate how much water that energy could boil. Using this metaphor, it takes less energy to crack a 228-bit RSA key than it does to boil a teaspoon of water, but the energy expended on breaking a 228-bit ECC key could boil all the water on Earth. The same level of security with RSA would require a key size of 2,380 bits.
Where Elliptic Curve Cryptography Is Used
As mentioned earlier, ECC’s smaller key size makes it a perfect fit for devices with low CPU and memory resources, such as mobile and IoT devices. This enables web and mobile app developers to build high-performance, low-latency websites and applications while still offering their users robust data security. ECC is frequently used to secure wireless mobile communication protocols like Bluetooth, Wi-Fi and Near Field Communication (NFC).
Here are a few more common use cases for ECC:
- Secure communication protocols: ECC is used in various secure communication protocols to provide encryption, digital signatures and key exchange. Examples include Transport Layer Security (TLS) used in secure web browsing, Secure Shell (SSH) for secure remote login and Virtual Private Networks (VPNs) for secure network communication.
- Cryptocurrency and blockchain technology: Many cryptocurrencies, including Bitcoin, Ethereum and Litecoin, utilize elliptic curve cryptography for generating public and private key pairs, as well as for signing transactions. ECC provides the cryptographic security needed for securing digital assets and ensuring the integrity of blockchain networks.
- Smart cards and embedded systems: ECC is commonly used for securing payment systems, access control systems, electronic passports and other applications that require secure and compact cryptographic solutions.
- Digital signatures and certificates: ECC can be used for generating digital signatures, which are used for verifying the authenticity and integrity of digital documents and messages. ECC-based digital signatures are also employed in Public Key Infrastructure (PKI) systems to issue and validate digital certificates.
While ECC is rather new compared to RSA, it enjoys broad standardization and support from private-sector organizations and industry bodies. For example, the U.S. National Institute of Standards and Technology (NIST) has standardized ECC in its suite of cryptographic algorithms. Additionally, ECC is supported by popular cryptographic libraries, programming languages and operating systems. This acceptance further promotes its adoption in various sectors such as finance, healthcare and government services.
Considering these factors, it is safe to say that elliptic curve cryptography is popular and widely used in a variety of applications and industries. Its efficiency, security and broad support have made it a trusted choice for secure communication and cryptographic operations.
 Cybersecurity
Cybersecurity 
