Czym jest kryptografia krzywych eliptycznych?

Kryptografia krzywych eliptycznych (ECC) to forma kryptografii klucza publicznego oparta na matematyce krzywych eliptycznych. Zapewnia bezpieczny sposób wykonywania operacji kryptograficznych, takich jak wymiana kluczy, podpisy cyfrowe i szyfrowanie. ECC jest alternatywą dla szyfrowania Rivest-Shamir-Adleman (RSA), które powstało w 1977 r.

Czytaj dalej, aby dowiedzieć się więcej o kryptografii krzywych eliptycznych i dlaczego jest ona uważana za najbezpieczniejszą formę szyfrowania.

Jaka jest różnica między szyfrowaniem ECC a szyfrowaniem RSA?

Przed omówieniem różnic między ECC i RSA należy zrozumieć, jak działają algorytmy kryptograficzne z kluczem publicznym. Najbardziej podstawowe algorytmy kryptograficzne są jak pułapki. Łatwo jest wpaść w pułapkę, ale bardzo trudno jest się wydostać, ponieważ pułapki działają tylko w jednym kierunku. Zatem, aby algorytm kryptograficzny był skuteczny i bezpieczny, zaszyfrowanie wiadomości musi być łatwe, ale odszyfrowanie jej bez klucza prawie niemożliwe.

Zarówno ECC, jak i RSA to algorytmy szyfrowania klucza publicznego, które wykorzystują wysoce zaawansowane funkcje matematyczne. Szyfrowanie klucza publicznego składa się z dwóch komponentów: klucza publicznego i klucza prywatnego. Klucz publiczny szyfruje wiadomość za pomocą algorytmu matematycznego w celu przekształcenia jej w bardzo dużą liczbę, która sprawia wrażenie losowej. Wiadomość może zostać odszyfrowana tylko za pomocą klucza prywatnego, który pobiera losowo pojawiającą się liczbę i stosuje inny algorytm, który po prostu ją odszyfrowuje.

Matematyka stosowana przez ECC i RSA jest tak złożona, że działania mogą rozwiązać wyłącznie komputery. Matematyka w algorytmie RSA wykracza poza zakres tego bloga, ale bezpieczeństwo RSA zależy od ogromnej trudności w rozkładaniu dużych liczb pierwszych na czynniki pierwsze.

Dla tych, którzy potrzebują odświeżenia, liczba taka jak 20 rozłożona na czynniki pierwsze wygląda następująco:

20 = 4 * 5 = 2 * 2 * 5 = 2² * 5

Łatwe, prawda? Teraz wyobraź sobie ten sam rodzaj rozpisania liczb dłuższych niż 100 cyfr. Dlatego nawet przy użyciu klucza publicznego obliczenie klucza prywatnego bez znajomości czynników pierwszych jest niezwykle trudne pod względem obliczeniowym.

Problemy z kryptografią RSA

Chociaż algorytm RSA jest dość solidny, nie jest pozbawiony wad.

Rozkład bardzo dużych liczb na czynniki pierwsze jest niezwykle trudny, ale łatwiejszy niż kiedyś. Rozkładanie na czynniki pierwsze jest podstawowym elementem rachunku różniczkowego i innych zaawansowanych działań matematycznych, więc matematycy od lat szukają sposobów na ułatwienie sobie tego zadania. Istnieją skuteczne algorytmy do rozkładania dużych liczb, takie jak ogólne sito ciała liczbowego (GNFS), które jest obecnie najlepiej znaną metodą rozkładania dużych liczb – powyżej 110 cyfr.

Tymczasem moc obliczeniowa rośnie w oszałamiającym tempie. Gordon Moore, współzałożyciel Intela, przewidywał w 1965 roku, że co rok lub co dwa lata liczba tranzystorów na mikrochipie będzie się podwajać. Hipoteza ta jest znana jako prawo Moore’a i od lat 70. XX w. faktycznie się sprawdziła. Moc obliczeniowa podwaja się co dwa lata, a cena za moc obliczeniową spada.

Ponieważ zasoby obliczeniowe potrzebne do rozłożenia na czynniki pierwsze bardzo dużych liczb stają się coraz łatwiej dostępne dla dużej grupy odbiorców (w tym cyberprzestępców), rozmiar kluczy RSA musi rosnąć, aby nadążyć za zmianami. Z tego powodu RSA ma dość powolne szyfrowanie i deszyfrowanie, co sprawia, że szyfrowanie dużych wiadomości, zwłaszcza na urządzeniach mobilnych, jest niewykonalne. RSA jest powszechnie używany do wymiany kluczy i podpisów cyfrowych, w których rzeczywiste dane są szyfrowane przy użyciu symetrycznych algorytmów szyfrowania z krótszymi kluczami sesji.

Kryptografia krzywych eliptycznych zapewnia lepsze bezpieczeństwo przy mniejszych długościach kluczy, co zwiększa wydajność pod względem obliczeń i wymagań przepustowości. Przeanalizujemy działanie ECC w następnej sekcji.

Jak działa kryptografia krzywych eliptycznych (ECC)?

ECC opiera się na innym obszarze zaawansowanej matematyki zwanym krzywymi eliptycznymi. Krzywa eliptyczna jest definiowana przez równanie w postaci y² = x³ + ax + b, gdzie a i b są stałymi, a krzywa jest definiowana w skończonym polu. Na wykresie wygląda to następująco:

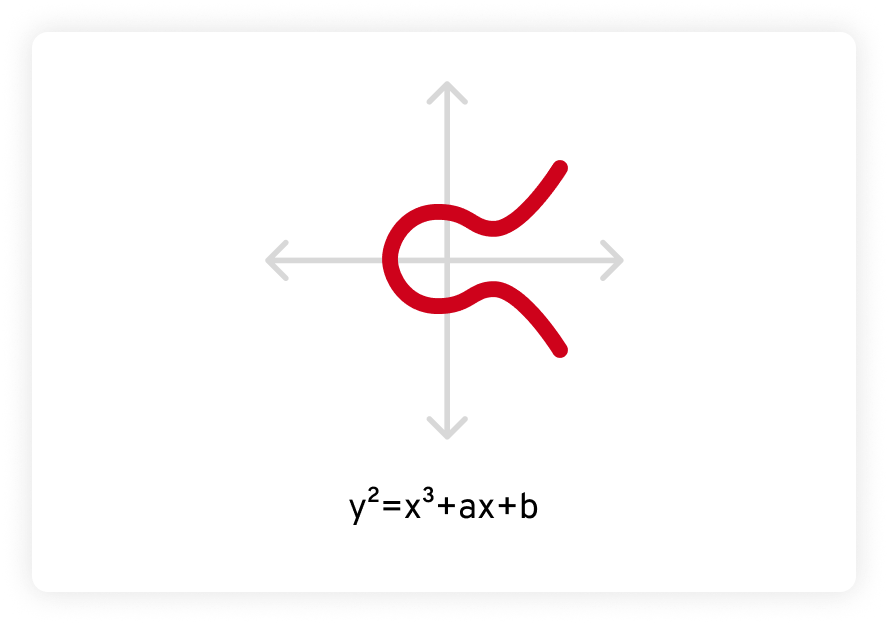
Krzywe eliptyczne mają pewne specjalne właściwości, które czynią je interesującymi i przydatnymi zarówno dla matematyków, jak i kryptografów. Po pierwsze, krzywe eliptyczne są symetryczne w płaszczyźnie poziomej. Po odbiciu na osi x (poziomej linii) obie strony są takie same jak odbicie lustrzane.

Ponadto każda niepionowa linia prosta przebiegająca przez krzywą eliptyczną zawsze przecina ją w co najwyżej trzech miejscach. W poniższym przykładzie punkty te są oznaczone jako P, Q i R.

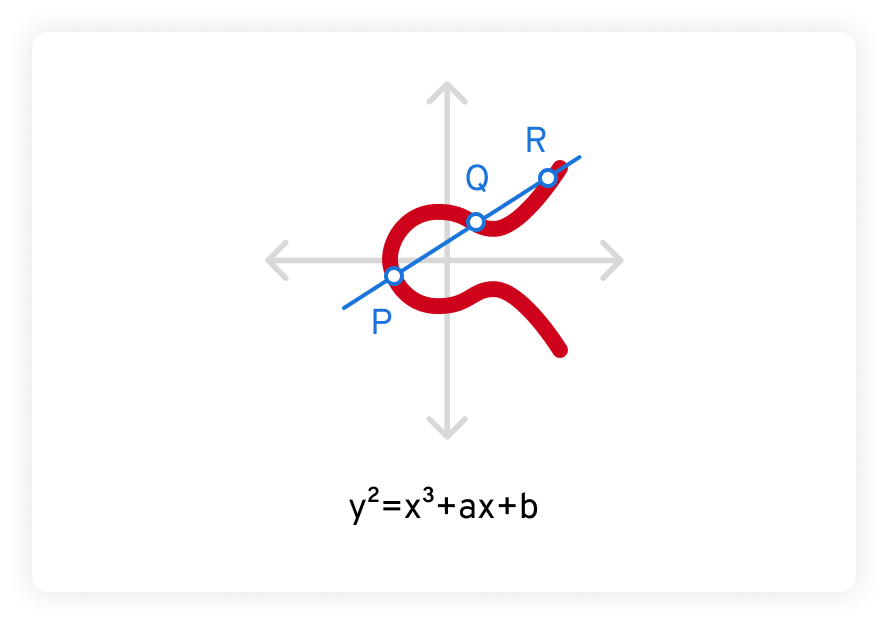
Bezpieczeństwo kryptografii krzywych eliptycznych jest pewne, ponieważ trudno jest rozwiązać problem dyskretnego logarytmu z krzywymi eliptycznymi. Biorąc pod uwagę punkt P na krzywej i skalar k, niezwykle trudno jest określić punkt Q tak, że Q = k*P – znacznie trudniej wykonać to działanie niż rozłożyć na czynniki pierwsze nawet bardzo dużą liczbę.

Ta właściwość oznacza, że ECC może zapewnić porównywalne lub nawet lepsze bezpieczeństwo niż RSA przy znacznie mniejszych rozmiarach kluczy.

Korzyści z kryptografii krzywych eliptycznych

Fakt, że ECC zapewnia bardzo wysoki poziom bezpieczeństwa przy użyciu krótkich kluczy, daje mu przewagę nad RSA i innymi algorytmami kryptograficznymi z kluczem publicznym.

Oto dwie korzyści wynikające z używania kryptografii krzywych eliptycznych.

• ECC wymaga mniejszej ilości zasobów obliczeniowych i mniejszej przepustowości do generowania, szyfrowania i deszyfrowania kluczy.
• Ze względu na mniejszy rozmiar klucza operacje ECC, takie jak generowanie kluczy, szyfrowanie i deszyfrowanie, mogą być wykonywane szybciej niż RSA, co oznacza mniejsze opóźnienia dla użytkownika końcowego.

Te zalety sprawiają, że ECC jest szczególnie przydatna w środowiskach z ograniczonymi zasobami, takich jak urządzenia mobilne i urządzenia Internetu rzeczy (IoT).

Jak bezpieczna jest kryptografia krzywych eliptycznych?

Chociaż algorytm szyfrowania RSA jest niezwykle bezpieczny, ECC jest prawdopodobnie jeszcze lepsza.

Komputery kwantowe teoretycznie mają potencjał łamania RSA poprzez skuteczne rozwiązanie problemu rozkładania na czynniki pierwsze, na którym opiera się RSA. Czy stanie się to w najbliższym czasie, jest przedmiotem wielkiej debaty. Jednak ze względu na złożoność szyfrowanie ECC jest bardziej odporne na ataki komputerów kwantowych w porównaniu z RSA.

Jak bardzo jest odporne? Holenderski matematyk Arjen Lenstra jest współautorem artykułu badawczego, w którym porównał łamanie algorytmów kryptograficznych do gotującej się wody. Chodzi o obliczenie ilości energii potrzebnej do złamania określonego algorytmu kryptograficznego, a następnie obliczenie ilości wody, jaką ta energia mogłaby doprowadzić do wrzenia. Używając tej metafory, złamanie 228-bitowego klucza RSA wymaga mniej energii niż zagotowanie wody na herbatę, ale energia zużyta na złamanie 228-bitowego klucza ECC może zagotować całą wodę na Ziemi. Ten sam poziom bezpieczeństwa w przypadku RSA wymaga klucza o rozmiarze 2380 bitów.

Gdzie stosuje się kryptografię krzywych eliptycznych?

Jak wspomniano wcześniej, mniejszy rozmiar klucza ECC sprawia, że idealnie pasuje do urządzeń o małej pojemności procesora i pamięci, takich jak urządzenia mobilne i urządzenia IoT. Umożliwia to twórcom aplikacji internetowych i mobilnych tworzenie wydajnych stron internetowych i aplikacji o niskich opóźnieniach, zapewniając jednocześnie użytkownikom solidne bezpieczeństwo danych. ECC jest często używana do zabezpieczania bezprzewodowych protokołów komunikacji mobilnej, takich jak Bluetooth, Wi-Fi i komunikacja bliskiego zasięgu (NFC).

Oto kilka typowych zastosowań ECC:

• Bezpieczne protokoły komunikacyjne: ECC jest używana w różnych bezpiecznych protokołach komunikacyjnych do szyfrowania, podpisów cyfrowych i wymiany kluczy. Są to między innymi zabezpieczenia warstwy transportowej (TLS) używane do bezpiecznego przeglądania stron internetowych, Secure Shell (SSH) do bezpiecznego logowania zdalnego oraz wirtualne sieci prywatne (VPN) do bezpiecznej komunikacji sieciowej.
• Kryptowaluty i technologia blockchain: Wiele kryptowalut, w tym Bitcoin, Ethereum i Litecoin, wykorzystuje kryptografię krzywych eliptycznych do generowania par kluczy publicznych i prywatnych, a także podpisywania transakcji. ECC zapewnia bezpieczeństwo kryptograficzne potrzebne do zabezpieczania cyfrowych zasobów i zapewnienia integralności sieci blockchain.
• Karty inteligentne i systemy wbudowane: ECC jest powszechnie używana do zabezpieczania systemów płatności, systemów kontroli dostępu, elektronicznych pasm i innych aplikacji, które wymagają bezpiecznych i kompaktowych rozwiązań kryptograficznych.
• Podpisy cyfrowe i certyfikaty: ECC może być używana do generowania podpisów cyfrowych, które służą do weryfikacji autentyczności oraz integralności dokumentów cyfrowych i wiadomości. Podpisy cyfrowe oparte na ECC są również wykorzystywane w systemach infrastruktury klucza publicznego (PKI) do wydawania i walidacji certyfikatów cyfrowych.

Chociaż ECC jest raczej nowym rozwiązaniem w porównaniu z RSA, cieszy się szeroką standaryzacją i wsparciem ze strony organizacji z sektora prywatnego i organizacji branżowych. Na przykład amerykański Krajowy Instytut Standardów i Technologii (NIST) ustandaryzował ECC w swoim zestawie algorytmów kryptograficznych. Ponadto ECC jest obsługiwana przez popularne biblioteki kryptograficzne, języki programowania i systemy operacyjne. Akceptacja ta dodatkowo sprzyja przyjęciu tego rozwiązania w różnych sektorach, takich jak finanse, opieka zdrowotna i usługi rządowe.

Biorąc pod uwagę te czynniki, można śmiało powiedzieć, że kryptografia krzywych eliptycznych jest popularna i szeroko stosowana w różnych aplikacjach i branżach. Jej skuteczność, bezpieczeństwo i szerokie wsparcie sprawiły, że jest to godny zaufania wybór w zakresie bezpiecznej komunikacji i operacji kryptograficznych.