¿Qué es la criptografía de curva elíptica?

La criptografía de curva elíptica (ECC, por sus siglas en inglés) es una forma de criptografía de clave pública que se basa en las matemáticas de las curvas elípticas. Ofrece una forma segura de realizar operaciones criptográficas, como el intercambio de claves, las firmas digitales y el cifrado. La ECC es una alternativa al cifrado de Rivest-Shamir-Adleman (RSA), que se lanzó por primera vez en 1977.

Siga leyendo para obtener más información sobre la criptografía de curva elíptica y por qué se considera la forma de cifrado más segura.

¿Cuál es la diferencia entre la ECC y la RSA?

Antes de ver las diferencias entre la ECC y la RSA, es importante comprender cómo funcionan los algoritmos criptográficos de clave pública. En su forma más básica, los algoritmos criptográficos sólidos son «funciones de trampilla». Si bien caer por una trampilla es muy sencillo, salir es muy difícil, porque las trampillas solo se abren en una dirección. Por lo tanto, para que un algoritmo criptográfico sea eficaz y seguro, debe ser fácil cifrar un mensaje, pero casi imposible de descifrar sin la clave de descifrado.

Tanto la ECC como la RSA son algoritmos de cifrado de clave pública que aprovechan funciones matemáticas altamente avanzadas. El cifrado de clave pública tiene dos componentes: una clave pública y una clave privada. La clave pública cifra un mensaje mediante la aplicación de un algoritmo matemático para transformarlo en un número muy grande y de apariencia aleatoria. El mensaje solo puede descifrarse con la clave privada, que toma el número que parece aleatorio y le aplica un algoritmo diferente que esencialmente «deshace» el original.

Las matemáticas que subyacen a la ECC y la RSA son tan complejas que solo pueden resolverse con ordenadores. Las matemáticas que subyacen en el algoritmo de la RSA van más allá del alcance de este blog, pero el quid de la cuestión es que la seguridad de la RSA depende de la inmensa dificultad de factorizar números muy grandes en los números primos que los componen.

Para quienes necesiten un repaso, factorizar un número como 20 es esto:

20 = 4 * 5 = 2 * 2 * 5 = 2² * 5

Parece simple, ¿verdad? Imagínese hacerlo con un número de más de 100 dígitos. Por eso, incluso con una clave pública, requiere mucha potencia computacional calcular la clave privada sin conocer los factores primos.

Problemas con la criptografía RSA

Si bien el algoritmo de la RSA es bastante sólido, no está exento de problemas.

Factorizar números muy grandes es extremadamente difícil, pero menos difícil de lo que solía ser. La factorización es un componente central del cálculo y de otras matemáticas avanzadas, por lo que los matemáticos llevan siglos buscando formas de hacerlo más fácil. Existen algoritmos eficientes para factorizar números grandes, como el Tamiz de campo numérico general, que actualmente es el método más conocido para factorizar números grandes que superen los 110 dígitos.

Mientras tanto, la potencia computacional crece a un ritmo asombroso. En 1965, el cofundador de Intel, Gordon Moore, predijo que el número de transistores en un microchip se duplicaría cada año o dos. Esta hipótesis se conoce como la ley de Moore y, desde la década de 1970, se ha cumplido o superado. La potencia informática se duplica aproximadamente cada dos años, y el precio de la potencia informática disminuye.

Dado que los recursos informáticos necesarios para factorizar números extremadamente grandes se vuelven más fáciles de conseguir y asequibles para una gran franja de público (incluidos los cibercriminales), los tamaños de las claves de la RSA deben crecer para mantenerse al día. Por ello, la RSA tiene velocidades de cifrado y descifrado bastante lentas, lo que hace que sea inviable cifrar mensajes de gran tamaño, especialmente en dispositivos móviles. En cambio, la RSA se utiliza comúnmente para el intercambio de claves y firmas digitales, donde los datos reales se cifran mediante algoritmos de cifrado simétricos con claves de sesión de menor duración.

Por el contrario, la criptografía de curva elíptica ofrece posiblemente una mejor seguridad con longitudes de clave más cortas, lo que la hace más eficiente en términos de requisitos de cálculo y ancho de banda. Examinaremos cómo funciona la ECC en la siguiente sección.

¿Cómo funciona la criptografía de curva elíptica?

La ECC se basa en otra área de las matemáticas avanzadas llamada curvas elípticas. Una curva elíptica se define mediante una ecuación de forma y² = x³ + ax + b, donde a y b son constantes y la curva se define sobre un campo finito. En un gráfico, se ve así:

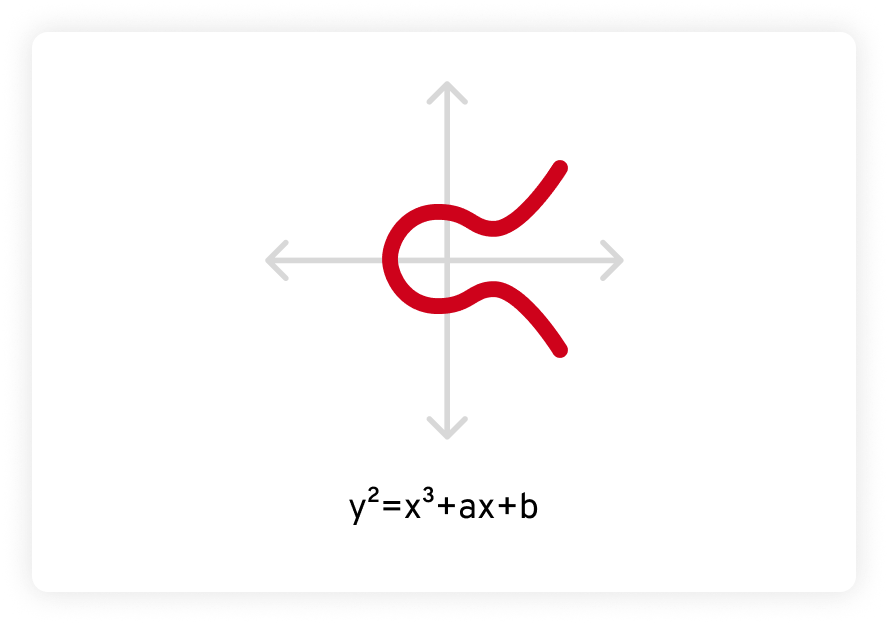
Las curvas elípticas tienen algunas propiedades especiales que las hacen interesantes y útiles tanto para matemáticos como para criptógrafos. En primer lugar, las curvas elípticas son horizontalmente simétricas. Cuando se reflejan sobre el eje x (la línea horizontal), ambos lados son iguales, como una imagen especular.

Además, cualquier línea recta no vertical dibujada a través de una curva elíptica siempre intersecará la curva en, como máximo, tres lugares. En el ejemplo que se muestra a continuación, esos puntos se etiquetan como P, Q y R.

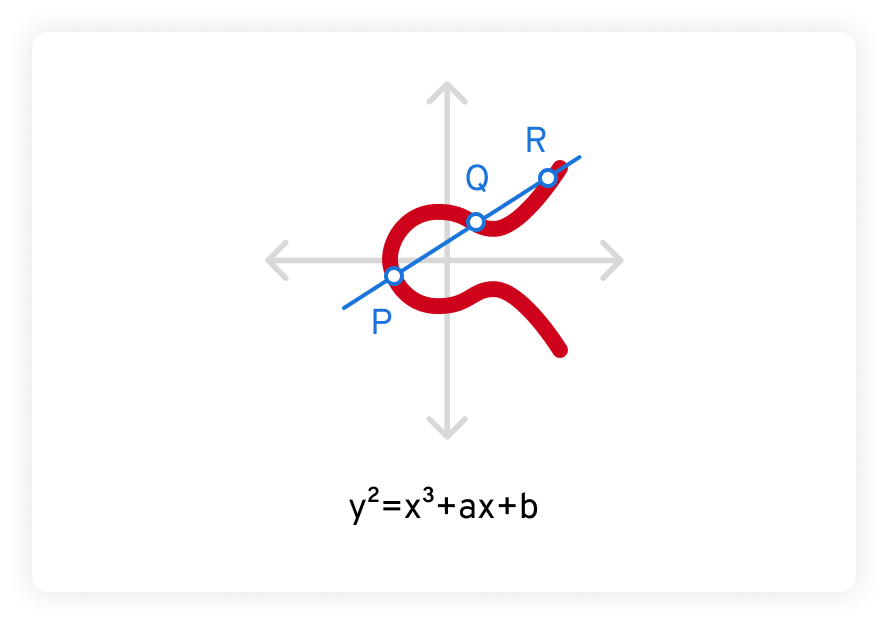
La seguridad de la criptografía de curva elíptica se basa en la dificultad de resolver lo que se conoce como el problema de logaritmo discreto de la curva elíptica. Dado un punto P en la curva y un escalar k, es extraordinariamente difícil determinar el punto Q de modo que Q = k*P, mucho más difícil que factorizar incluso un número muy grande.

Esta propiedad significa que la ECC puede ofrecer una seguridad comparable o incluso mejor que la RSA con tamaños de clave mucho más bajos.

Ventajas de la criptografía de curva elíptica

El hecho de que la ECC ofrezca un nivel muy alto de seguridad con longitudes de clave cortas le da ventajas sobre la RSA y otros algoritmos de criptografía de clave pública.

He aquí dos ventajas de utilizar la criptografía de curva elíptica.

• La ECC requiere menos recursos computacionales y menos ancho de banda para la generación, el cifrado y el descifrado de claves.
• Debido al tamaño de la clave más pequeño de la ECC, las operaciones de ECC, como la generación de claves, el cifrado y el descifrado, pueden realizarse más rápido en comparación con la RSA, lo que significa menos latencia para el usuario final.

Estas ventajas hacen que la ECC sea particularmente útil en entornos con recursos limitados, como los dispositivos móviles y el Internet de las cosas (IoT).

¿Cómo de segura es la criptografía de curva elíptica?

Si bien el algoritmo de cifrado RSA es extremadamente seguro, la ECC es posiblemente incluso mejor.

Los ordenadores cuánticos tienen teóricamente el potencial de descifrar la RSA al resolver de forma eficiente el problema de factorización en el que se basa la RSA. Que esto suceda a corto plazo es objeto de grandes debates. Sin embargo, es seguro decir que, debido a la complejidad de la ECC, es más resistente a los ataques de computación cuántica en comparación con la RSA.

¿Cuánto más resistente? El matemático holandés Arjen Lenstra coescribió un artículo de investigación que comparaba la descomposición de los algoritmos criptográficos con el agua hirviendo. La idea es calcular cuánta energía se requiere para descifrar un algoritmo criptográfico específico y luego calcular cuánta agua podría hervir con esa energía. Utilizando esta metáfora, se necesita menos energía para descifrar una clave RSA de 228 bits que para hervir una cucharilla de té de agua, pero la energía necesaria para descifrar una clave ECC de 228 bits podría hacer hervir toda el agua de la Tierra. El mismo nivel de seguridad con la RSA requeriría un tamaño de clave de 2380 bits.

Dónde se utiliza la criptografía de curva elíptica

Como dijimos anteriormente, el tamaño menor de la clave de la ECC la hace perfecta para dispositivos con pocos recursos de CPU y memoria, como los dispositivos móviles y el IoT. Esto permite a los desarrolladores de aplicaciones web y móviles crear sitios web y aplicaciones de alto rendimiento y baja latencia, al tiempo que ofrece a sus usuarios una seguridad de datos sólida. La ECC se suele utilizar para proteger los protocolos de comunicación móvil inalámbrica como Bluetooth, wifi y la comunicación de campo cercano (NFC).

He aquí algunos de los casos de uso más comunes de la ECC:

• Protocolos de comunicación seguros: la ECC se utiliza en varios protocolos de comunicación seguros para proporcionar cifrado, firmas digitales e intercambio de claves. Algunos ejemplos son la seguridad de la capa de transporte (TLS) que se utiliza en la navegación web segura, el intérprete de órdenes seguro (SSH) para inicio de sesión remoto seguro y las redes privadas virtuales (VPN) para una comunicación de red segura.
• Tecnología de criptomonedas y cadena de bloques: muchas criptomonedas, como Bitcoin, Ethereum y Litecoin, utilizan la criptografía de curva elíptica para generar pares de claves públicas y privadas, así como para firmar transacciones. La ECC ofrece la seguridad criptográfica necesaria para proteger los conjuntos digitales y garantizar la integridad de las redes de cadena de bloques.
• Tarjetas inteligentes y sistemas integrados: la ECC se utiliza comúnmente para proteger los sistemas de pago, los sistemas de control de acceso, los pasaportes electrónicos y otras aplicaciones que requieren soluciones criptográficas seguras y compactas.
• Firmas y certificados digitales: la ECC se puede utilizar para generar firmas digitales, que se utilizan para verificar la autenticidad y la integridad de los documentos y mensajes digitales. Las firmas digitales basadas en la ECC también se utilizan en los sistemas de infraestructura de clave pública (PKI) para emitir y validar certificados digitales.

Si bien la ECC es bastante reciente en comparación con la RSA, goza de una amplia estandarización y del apoyo de las organizaciones del sector privado y los organismos del sector. Por ejemplo, el Instituto Nacional de Normas y Tecnología de los Estados Unidos (NIST) ha estandarizado la ECC en su conjunto de algoritmos criptográficos. Además, la ECC es compatible con bibliotecas criptográficas, lenguajes de programación y sistemas operativos populares. Esta aceptación promueve aún más su adopción en varios sectores, como las finanzas, la atención médica y los servicios gubernamentales.

Teniendo en cuenta estos factores, es seguro decir que la criptografía de curva elíptica es popular y ampliamente utilizada en diversas aplicaciones y sectores. Su eficiencia, seguridad y un amplio soporte la han convertido en una opción de confianza para las operaciones criptográficas y de comunicación seguras.